What we often refer to as the sorting algorithm is often referred to as an internal sorting algorithm, ie data records are sorted in memory.
Sorting algorithms can be roughly divided into two types:
One is the comparative sorting, the time complexity O(nlogn) ~ O(n^2), mainly include: bubble sort, select sort, insert sort, merge sort, heap sort, quick sort and so on.
The other is non-comparative sorting, and the time complexity can reach O(n), mainly including: count sort, base sort, bucket sort, and so on.
Here we discuss the commonly used comparison sorting algorithm, non-comparison sorting algorithm will be introduced in the next article. The following table shows the performance of common comparison sorting algorithms:
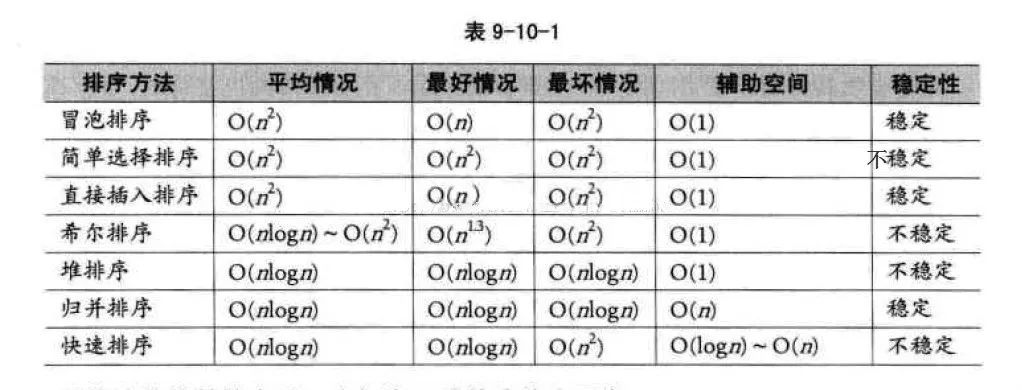
One thing we can easily overlook is the stability of the sorting algorithm.
The simple formalization of the sorting algorithm's stability is defined as: If Ai = Aj, Ai is prior to Aj before sorting, and Ai is still before Aj after sorting, the sorting algorithm is said to be stable. In layman's terms, the relative order of two equal numbers before and after sorting is guaranteed.
For an unstable sorting algorithm, as long as an example is given, its instability can be illustrated; and for a stable sorting algorithm, an algorithm must be analyzed to obtain a stable characteristic. It should be noted that whether or not the sorting algorithm is stable is determined by a specific algorithm. An unstable algorithm can become a stable algorithm under certain conditions, and a stable algorithm can also become unstable under certain conditions. algorithm.
For example, for bubbling ordering, which is originally a stable sorting algorithm, if the record exchange condition is changed to A[i] >= A[i + 1], two equal records will be swapped and become no Stable sorting algorithm.
Second, talk about the benefits of sorting algorithm stability. If the sorting algorithm is stable, then sorting from one key, and then sorting from another key, the result of the previous key sort can be used for the next key sort. This is the case for cardinality sorting. First, sort by low order, and then sort by high order, and then the order of the elements after the low order is not changed when the high order is also the same.
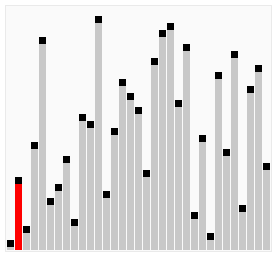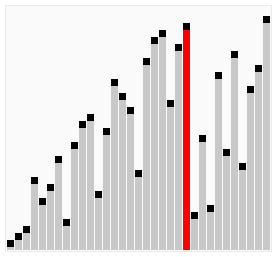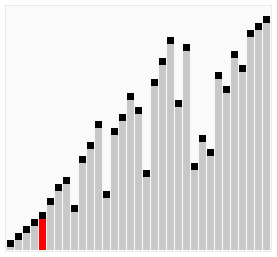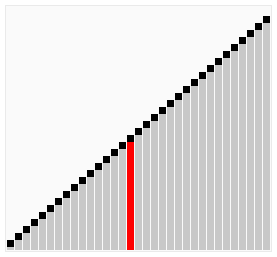
Bubble Sort
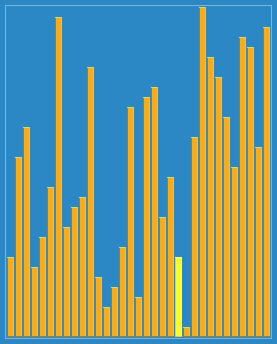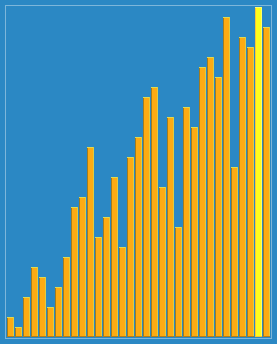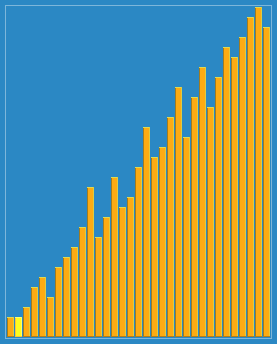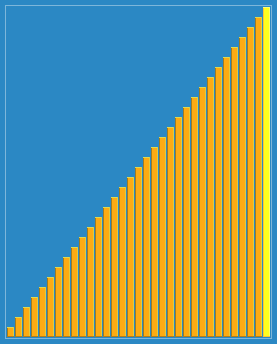
Bubble sorting is an extremely simple sorting algorithm and the first sorting algorithm I learned. It repeatedly visited the elements to be sorted, followed by comparing two adjacent elements, and if they were in the wrong order, they would be swapped in until they had no elements to exchange, and the sorting was completed. The name of this algorithm is derived because the smaller (or larger) elements slowly "float" through the exchange to the top of the series.
The bubble sort algorithm works as follows:
Compare adjacent elements. If the previous one is bigger than the latter one, swap the two of them.
Do the same for each pair of adjacent elements, starting with the first pair and ending with the last pair. After this step is done, the final element will be the largest number.
Repeat the above steps for all elements except the last one.
Repeat the above steps for fewer and fewer elements at a time until no pair of numbers need to be compared.
Due to its simplicity, Bubble Sort is often used to introduce the concept of algorithms to students of programming. Bubble sorting code is as follows:
#include
// Classification -------------- Internal comparison
// data structure ---------- array
// Worst time complexity ---- O(n^2)
// Optimal time complexity ---- If you can use the internal flag for the first time when the internal loop is running, you can use a flag to indicate if there is a need for swapping. You can reduce the optimal time complexity to O(n).
// The average time complexity ---- O(n^2)
// Required auxiliary space ------ O(1)
// Stability ------------ Stable
voidSwap(intA[],inti,intj)
{
Inttemp=A[i];
A[i]=A[j];
A[j]=temp;
}
voidBubbleSort(intA[],intn)
{
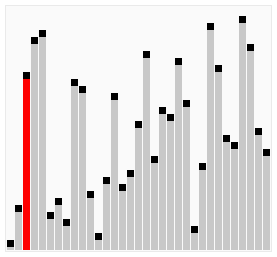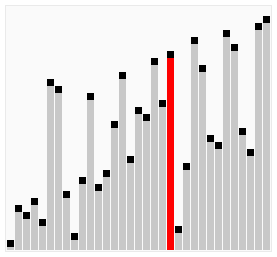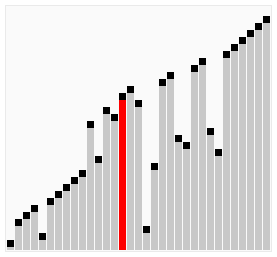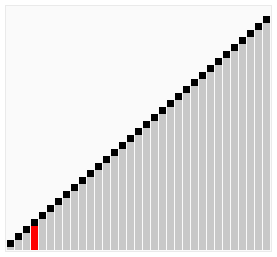
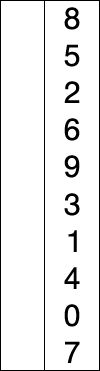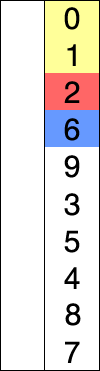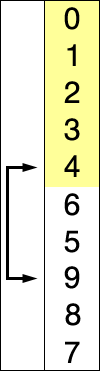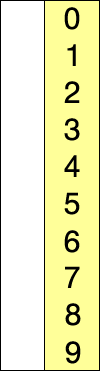
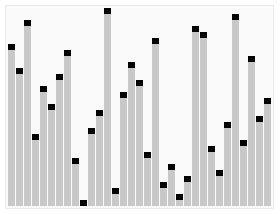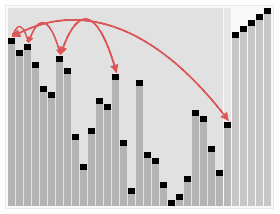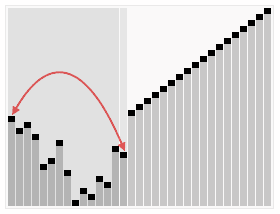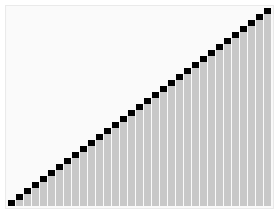
For(intj=0;j { For(inti=0;i { If(A[i]>A[i+1]) // If the condition is changed to A[i] >= A[i + 1], it becomes an unstable sorting algorithm { Swap(A,i,i+1); } } } } Intmain() { intA[]={6,5,3,1,8,7,2,4}; // Bubble sorting from small to big Intn=sizeof(A)/sizeof(int); BubbleSort(A,n); Printf("bubble sort result:"); For(inti=0;i { Printf("%d ",A[i]); } Printf(" "); Return0; } The above code performs a bubble sort on the sequence { 6, 5, 3, 1, 8, 7, 2, 4} as follows: The process of sorting a list of numbers using a bubble sort is shown in the right figure: Although bubble ordering is one of the sorting algorithms that is the easiest to understand and implement, it is inefficient for sorting out a few elements. Bubble Sorting Improvements: Cocktail Sorting Cocktail sorting, also called directed bubble sorting, is an improvement over bubble sorting. The difference between this algorithm and bubble sort is from low to high and then high to low, while bubble sort only compares each element in the sequence from low to high. He can get slightly better performance than bubble sort. The code for cocktail sorting is as follows: #include // Classification -------------- Internal comparison // data structure ---------- array // Worst time complexity ---- O(n^2) // Optimal time complexity ---- If the sequence has been mostly sorted at the beginning, it will be close to O(n) // The average time complexity ---- O(n^2) // Required auxiliary space ------ O(1) // Stability ------------ Stable voidSwap(intA[],inti,intj) { Inttemp=A[i]; A[i]=A[j]; A[j]=temp; } voidCocktailSort(intA[],intn) { Intleft=0; // Initialize the boundary Intright=n-1; While(left { For(inti=left;i { If(A[i]>A[i+1]) { Swap(A,i,i+1); } } Right--; For(inti=right;i>left;i--) // In the second half, put the smallest element in front { If(A[i-1]>A[i]) { Swap(A,i-1,i); } } Left++; } } Intmain() { intA[]={6,5,3,1,8,7,2,4}; // Small to large directional bubble sort Intn=sizeof(A)/sizeof(int); CocktailSort(A,n); Printf("Cocktail sort result:"); For(inti=0;i { Printf("%d ",A[i]); } Printf(" "); Return0; } The process of sorting a list of numbers using a cocktail order is shown in the right figure: Taking the sequence (2,3,4,5,1) as an example, the sorting of the cocktails only needs to visit the first sequence to complete the sorting, but if using the bubble sort it takes four times. However, in the random number sequence, the efficiency of cocktail sorting and bubble sorting is poor. Selection Sort Selecting sorting is also a simple and intuitive sorting algorithm. Its working principle is easy to understand: Initially find the smallest (large) element in the sequence, place it at the beginning of the sequence as the sorted sequence; then, continue to search for the smallest (large) element from the remaining unsorted elements. To the end of the sorted sequence. And so on, until all elements are sorted. Note the difference between sorting and bubble sorting: bubble sorting places the current smallest (large) element in place by sequentially swapping the positions of two adjacent invalid elements, while selecting the sort is remembered once per traversal. The location of the current smallest (large) element, and finally it can be placed in the right place with only one exchange operation. The sorting code is as follows: #include // Classification -------------- Internal comparison // data structure ---------- array // Worst time complexity ---- O(n^2) // Optimal time complexity ---- O(n^2) // The average time complexity ---- O(n^2) // Required auxiliary space ------ O(1) // Stability ------------ Instability voidSwap(intA[],inti,intj) { Inttemp=A[i]; A[i]=A[j]; A[j]=temp; } voidSelectionSort(intA[],intn) { For(inti=0;i { Intmin=i; For(intj=i+1;j { If(A[j] { Min=j; } } If(min!=i) { Swap(A,min,i); // put at the end of the sorted sequence, this operation is very likely to upset the stability, so the selection order is an unstable sorting algorithm } } } Intmain() { intA[]={8,5,2,6,9,3,1,4,0,7};// Sorting from small to large Intn=sizeof(A)/sizeof(int); SelectionSort(A,n); Printf("select sort result:"); For(inti=0;i { Printf("%d ",A[i]); } Printf(" "); Return0; } The implementation of the above code selection sequence for the sequence {8, 5, 2, 6, 9, 3, 1, 4, 0, 7} is as shown in the right figure: The macro process of using sorting to sort a list of numbers: Selecting ordering is an unstable sorting algorithm. The instability occurs when the minimum element exchanges with A[i]. For example, the sequence: { 5, 8, 5, 2, 9 }, the smallest element chosen at a time is 2, and then swaps 2 with the first 5, thus changing the relative order of the two elements 5. Insertion Sort Insert sorting is a simple and intuitive sorting algorithm. It works very much like we grab poker For unsorted data (cards caught in the right hand), scan backwards and forwards in the sorted sequence (left-handed ordered hands) to find the corresponding position and insert. Insertion sorting is usually implemented in an in-place ordering (that is, only the extra space of O(1) is used for the sorting). Therefore, it is necessary to repeatedly shift the sorted elements backwards and forwards during scanning from back to front. , provides insertion space for the latest elements. The specific algorithm is described as follows: Beginning with the first element, this element can be considered sorted Takes the next element and scans backwards from the back in the sequence of elements already sorted If the element (sorted) is larger than the new element, move the element to the next position Repeat step 3 until you find that the sorted element is less than or equal to the new element's position Insert new element into this position Repeat steps 2~5 Insert the sorted code as follows: #include // Classification ------------- Internal comparison // data structure ---------- array // Worst time complexity ---- worst case input sequence is descending, time complexity O(n^2) // Optimal time complexity ---- The best case is that the input sequence is in ascending order, and the time complexity O(n) // The average time complexity ---- O(n^2) // Required auxiliary space ------ O(1) // Stability ------------ Stable voidInsertionSort(intA[],intn) { For(inti=1;i { Intget=A[i]; // The right hand catches a playing card Intj=i-1; // The cards in the left hand are always sorted well While(j>=0&&A[j]>get) // Compare the captured card with the hand from right to left { A[j+1]=A[j]; // If the hand is bigger than the card it grabs, move it right J--; } A[j+1]=get;// Until the hand is smaller (or equal) than the card caught, insert the card that is caught to the right of the hand (the relative order of the equal elements is not changed, so insert Sorting is stable) } } Intmain() { intA[]={6,5,3,1,8,7,2,4} ;// Insert from small to large Intn=sizeof(A)/sizeof(int); InsertionSort(A,n); Printf("insert sort result:"); For(inti=0;i { Printf("%d ",A[i]); } Printf(" "); Return0; } The above code implementation sequence for inserting the sequence { 6, 5, 3, 1, 8, 7, 2, 4 } is as follows: The macro process of sorting a list of numbers using insert sorting: Insert sorting is not suitable for sorting applications with a large amount of data. However, if the amount of data that needs to be sorted is small, for example, if the magnitude is less than a thousand, insert sorting is still a good choice. Insertion sorting is also widely used in industrial-level libraries. In both the STL sort algorithm and the stdlib qsort algorithm, insert-ordering is used as a supplement to quick sorting, and is used to sort small numbers of elements (usually 8 or less). Insert sorting improvements: two-point insertion sort For insertion sorting, if the cost of the comparison operation is greater than the exchange operation, the binary search method can be used to reduce the number of comparison operations. We call it a two-division insertion order. The code is as follows: #include // Classification -------------- Internal comparison // data structure ---------- array // Worst time complexity ---- O(n^2) // Optimal time complexity ---- O(nlogn) // The average time complexity ---- O(n^2) // Required auxiliary space ------ O(1) // Stability ------------ Stable voidInsertionSortDichotomy(intA[],intn) { For(inti=1;i { Intget=A[i]; // The right hand catches a playing card Intleft=0; // The cards on the left hand are always sorted so that you can use the dichotomy. Intright=i-1; // The left and right hand cards are initialized While(left<=right) // Position the new card using dichotomy { Intmid=(left+right)/2; If(A[mid]>get) Right=mid-1; Else Left=mid+1; } For(intj=i-1;j>=left;j--) // move the card to the right of the new card position by one unit to the right { A[j+1]=A[j]; } A[left]=get; // Insert the caught card into the hand } } Intmain() { intA[]={5,2,9,4,7,6,1,3,8};//Insert sort from small to large Intn=sizeof(A)/sizeof(int); InsertionSortDichotomy(A,n); Printf ("two-insert insertion sort result:"); For(inti=0;i { Printf("%d ",A[i]); } Printf(" "); Return0; } When n is large, the number of comparisons of binary insertion sorting is much better than the worst case of direct insertion sorting, but it is worse than the best case of direct insertion sorting. When the initial sequence of elements is close to ascending order, direct insertion sorting Less than two-insertion sort comparisons. Binary insert sort elements move the same number of times as the direct insert sort, depending on the element's initial sequence. More efficient insertion sorting improvements: Shell Sort Hill sorting, also called decremental incremental sorting, is a more efficient and improved version of insert sorting. Hill sequencing is an unstable sorting algorithm. Hill sorting is based on the following two properties of the insertion order and proposes an improved method: Insertion sorting is efficient when operating on almost-ordered data, ie it can achieve linear sorting efficiency But insert sorting is generally inefficient because insert sorting can only move data one bit at a time Hill sequencing improves the performance of insertion sequencing by dividing all the elements of the comparison into several regions. This allows one element to move one step toward the final position in one go. The algorithm then takes smaller and smaller steps to sort. The final step of the algorithm is the normal insertion ordering. However, at this step, the data to be sorted is almost always scheduled (in this case, the insert sorting is faster). Suppose there is a small amount of data at the end of an array that has been sorted in ascending order. If the order is complexity O(n^2) (bubble ordering or inline sorting), n comparisons and exchanges may be performed to move the data to the correct position. Hill sorting moves the data in larger steps, so small data can be moved to the right place with only a few comparisons and exchanges. Hill sorts the code as follows: #include // Classification -------------- Internal comparison // data structure ---------- array // The worst time complexity---- varies according to the sequence of steps. The best known O(n(logn)^2) // Optimal time complexity ---- O(n) // The average time complexity---- varies according to the sequence of steps. // Required auxiliary space ------ O(1) // Stability ------------ Instability voidShellSort(intA[],intn) { Inth=0; While(h<=n) // Generate initial increments { h=3*h+1; } While(h>=1) { For(inti=h;i { Intj=ih; Intget=A[i]; While(j>=0&&A[j]>get) { A[j+h]=A[j]; j=jh; } A[j+h]=get; } h=(h-1)/3; // decrement incrementally } } Intmain() { intA[]={5,2,9,4,7,6,1,3,8};// Sorting from small to large Intn=sizeof(A)/sizeof(int); ShellSort(A,n); Printf("Hill sort result:"); For(inti=0;i { Printf("%d ",A[i]); } Printf(" "); Return0; } Sort the hills in steps of 23, 10, 4, 1: Hill sorting is an unstable sorting algorithm. Although one insert sorting is stable and does not change the relative order of the same elements, in the different insert sorting processes, the same elements may move in their respective insert sorts, and finally they are stable. Sex will be disrupted. For example, the sequence is: {3, 5, 10, 8, 7, 2, 8, 1, 20, 6}. When h=2, it is divided into two subsequences {3, 10, 7, 8, 20} and { 5, 8, 2, 1, 6 }, 8 in front of the second subsequence before being sorted, now inserts the two subsequences into order, getting { 3, 7, 8, 10, 20 } and { 1, 2, 5, 6 8}, ie {3, 1, 7, 2, 8, 5, 10, 6, 20, 8}, the relative order of the two 8s has changed. Merge Sort Merging ordering is an effective sorting algorithm created on the merge operation with an efficiency of O(nlogn). It was first proposed by von Neumann in 1945. The implementation of merge sort is divided into recursive implementation and non-recursive (iterative) implementation. The recursive implementation merge sort is a typical application of the divide-and-conquer strategy in algorithm design. We divide a big problem into small problems and solve them separately. Then we use the answers of all small problems to solve the big problem. The non-recursive (iterative) implementation of the merge sort is first performed in pairs, then merged in fours and fours, then merged in eights and eights, and continued until the entire array is merged. Merge sorting algorithms mainly rely on Merge operations. Merging operation refers to the operation of merging two already sorted sequences into a sequence. The merging steps are as follows: Apply space to the size of the sum of the two sorted sequences used to store the merged sequence Set two pointers, the initial position is the starting position of two already sorted sequences Compare the elements pointed to by two pointers, select relatively small elements to put into the merge space, and move the pointer to the next position Repeat step 3 until some pointer reaches the end of the sequence Copy all the remaining elements of another sequence directly to the end of the merge sequence The merged sort code is as follows: #include #include // Classification -------------- Internal comparison // data structure ---------- array // Worst time complexity ---- O(nlogn) // Optimal time complexity ---- O(nlogn) // Average time complexity ---- O(nlogn) // Required auxiliary space ------ O(n) // Stability ------------ Stable voidMerge(intA[],intleft,intmid,intright) // Merge two sorted arrays A[left...mid] and A[mid+1...right] { Intlen=right-left+1; Int*temp=newint[len]; // auxiliary space O(n) Intindex=0; Inti=left; // The starting element of the previous array Intj=mid+1; // The starting element of the next array While(i<=mid&&j<=right) { Temp[index++]=A[i]<=A[j]?A[i++]:A[j++]; // Guaranteed the stability of merging and sorting with equal signs } While(i<=mid) { Temp[index++]=A[i++]; } While(j<=right) { Temp[index++]=A[j++]; } For(intk=0;k { A[left++]=temp[k]; } } Void MergeSortRecursion(intA[],intleft,intright) // recursive merge sort (top down) { If(left==right) // When the length of the sequence to be sorted is 1, the recursion starts backtracking and the merge operation is performed. Return; Intmid=(left+right)/2; MergeSortRecursion(A,left,mid); MergeSortRecursion(A,mid+1,right); Merge(A,left,mid,right); } voidMergeSortIteration(intA[],intlen) // Merge ordering of non-recursive (iterative) implementations (bottom up) { Intleft, mid, right;// sub-array index, the former is A[left...mid], the latter sub-array is A[mid+1...right] For(inti=1;i { Left=0; While(left+i { Mid=left+i-1; Right=mid+i Merge(A,left,mid,right); Left=right+1; // Previous subarray index moves backward } } } Intmain() { intA1[]={6,5,3,1,8,7,2,4}; // Sorting from small to large intA2[]={6,5,3,1,8,7,2,4}; Intn1=sizeof(A1)/sizeof(int); Intn2=sizeof(A2)/sizeof(int); MergeSortRecursion(A1,0,n1-1); // Recursive implementation MergeSortIteration(A2,n2); // Non-recursive implementation Printf("recursive implementation merge sort result:"); For(inti=0;i { Printf("%d ",A1[i]); } Printf(" "); Printf ("non-recursive implementation of merged sort results:"); For(inti=0;i { Printf("%d ",A2[i]); } Printf(" "); Return0; } An example of merging the sequence { 6, 5, 3, 1, 8, 7, 2, 4 } by the above code is as follows The macro process of sorting a list of numbers using merge sort: In addition to sorting arrays, merge sorting can efficiently find array sums (ie monotonic sums) and reversed pairs in arrays. See this blog post for details. Heap Sort Heap sorting refers to a sorting algorithm designed using a heap data structure. The heap is an almost complete binary tree structure (usually the heap is implemented by a one-dimensional array) and satisfies the nature: Take the largest heap (also called big root heap, big top heap) as an example, where the value of the parent node is always Greater than its child nodes. We can easily define the heap sorting process: Construct a maximum heap from the input unordered array as the initial unordered area Interchange the top element (maximum) and tail element Reduce the size of the heap (unordered area) by 1 and call heapify(A, 0) to start heap adjustment from the new heap top element Repeat step 2 until the heap size is 1 The heap sorting code is as follows: #include // Classification -------------- Internal comparison // data structure ---------- array // Worst time complexity ---- O(nlogn) // Optimal time complexity ---- O(nlogn) // Average time complexity ---- O(nlogn) // Required auxiliary space ------ O(1) // Stability ------------ Instability voidSwap(intA[],inti,intj) { Inttemp=A[i]; A[i]=A[j]; A[j]=temp; } voidHeapify(intA[],inti,intsize) // Heap adjustment from A[i] down { Intleft_child=2*i+1; // left child index Intright_child=2*i+2; // right child index Intmax=i; // Select the maximum of the current node and the child If(left_child Max=left_child; If(right_child Max=right_child; If(max!=i) { Swap(A,i,max); // Exchange the current node with its largest (direct) child node Heapify(A,max,size); // Call recursively, continue down heap adjustment from current node } } intBuildHeap(intA[],intn) // Build heap, time complexity O(n) { Intheap_size=n; For(inti=heap_size/2-1;i>=0;i--)// Heap adjustment starting from each non-leaf node Heapify(A,i,heap_size); Returnheap_size; } voidHeapSort(intA[],intn) { Intheap_size=BuildHeap(A,n); // Create a max heap While(heap_size>1) // The number of elements in the heap (unordered area) is greater than 1 and the sort is not completed. { // Interchange the top element of the heap with the last element of the heap and remove the last element from the heap // The swap operation here is very likely to upset the stability of the following elements, so the heap sort is an unstable sort algorithm Swap(A,0,--heap_size); Heapify(A,0,heap_size); // Heap adjustment starting from the new heap top element, time complexity O(logn) } } Intmain() { intA[]={5,2,9,4,7,6,1,3,8} ;// Sort from small to large Intn=sizeof(A)/sizeof(int); HeapSort(A,n); Printf("heap sort result:"); For(inti=0;i { Printf("%d ",A[i]); } Printf(" "); Return0; } Demonstration of heap sort algorithm: The animation simply shows the process of creating the heap and the logical structure of the heap before the sorting process. Heap sorting is an unstable sorting algorithm. The instability occurs at the moment when the top element of the heap exchanges with A[i]. For example, the sequence: {9, 5, 7, 5}, the top element of the heap is 9, and the heap will be sorted next. 9 and the second 5 will be exchanged, and the sequence {5, 5, 7, 9} will be obtained, and then the stack will be adjusted. {7, 5, 5, 9}, repeat the previous operation to get {5, 5, 7, 9} thus changing the relative order of the two 5s. Quick Sort Quick sorting is a sorting algorithm developed by Tony Hall. In the average condition, sort n elements to O(nlogn) times. In the worst case, O(n^2) comparisons are needed, but this situation is not common. In fact, quick sorting is usually significantly faster than other O(nlogn) algorithms because its internal loop can be efficiently implemented on most architectures. Quick sort uses Divide and Conquer to divide a sequence into two subsequences. The steps are: Pick an element from the sequence as a "pivot". All elements smaller than the reference value are placed in front of the reference, and all elements larger than the reference value are placed behind the reference (the same number can go to either side). This is called a partition operation. Steps 1 to 2 are recursively performed for each partition. The recursive end condition is that the size of the sequence is 0 or 1, and the whole is already sorted. The quick ordering code is as follows: #include // Classified ------------ Internal Compare Sort // data structure --------- array // Worst time complexity - Each time the selected reference is the largest (or smallest) element, resulting in only one partition at a time, n-1 partitions are needed to end the recursion. Time complexity O(n^2) // Optimal time complexity ---- Each time you select the benchmark is a median, so that each time you divide the two partitions evenly, you only need logn times to end the recursion. The time complexity is O ( Nlogn) // Average time complexity ---- O(nlogn) // The required auxiliary space ------ is mainly due to the use of the stack space caused by recursion (used to save local variables such as left and right), depending on the depth of the recursive tree, generally O (logn), the worst O(n) // stability ---------- unstable voidSwap(intA[],inti,intj) { Inttemp=A[i]; A[i]=A[j]; A[j]=temp; } intPartition(intA[],intleft,intright) // Dividing function { Intpivot=A[right]; // This selects the last element as a reference Inttail=left-1; // tail is the index of the last element of the sub-array that is smaller than the reference For(inti=left;i { If(A[i]<=pivot) // Put the elements less than or equal to the reference at the end of the previous subarray { Swap(A,++tail,i); } } Swap(A,tail+1,right); // Finally, the reference is placed behind the previous subarray. The remaining subarrays are both subarrays larger than the reference. // This operation is very likely to disturb the stability of the following elements, so quick sorting is an unstable sorting algorithm Returntail+1; // Returns the index of the benchmark } voidQuickSort(intA[],intleft,intright) { If(left>=right) Return; Intpivot_index=Partition(A,left,right);// The index of the datum QuickSort(A,left,pivot_index-1); QuickSort(A,pivot_index+1,right); } Intmain() { intA[]={5,2,9,4,7,6,1,3,8};// Quick sort from small to big Intn=sizeof(A)/sizeof(int); QuickSort(A,0,n-1); Printf("Quick sort result:"); For(inti=0;i { Printf("%d ",A[i]); } Printf(" "); Return0; } The process of sorting a list of numbers using quick sorting: Quick sorting is an unstable sorting algorithm. The instability occurs when the reference element and A[tail+1] are exchanged. For example, the sequence: { 1, 3, 4, 2, 8, 9, 8, 7, 5 }, the reference element is 5, and 5 is to be exchanged with the first 8 after a division operation, thus changing two elements 8 Relative order. The Arrays.sort function provided by the Java system. For basic types, the bottom layer uses quick sorting. For non-basic types, the underlying uses merge sort. Why is this? A: This is in consideration of the stability of the sorting algorithm. For the basic type, the same value is no difference, the relative position of the same value before and after sorting is not important, so choose a more efficient quick sort, although it is an unstable sort algorithm; and for non-basic types, sort before and after the equal instance The relative position should not be changed, so choose a stable merge sort.
MARSHINE SDM series ground anchor is a tool for temporary anchorage during the transmission line construction. It serves to fix the winch, puller tensioner, turning block, and the temporary guy wire, among others.
This product is designed with the steel plate welded structure. Its surface is coated with the antirust paint, thus offering high durability.
Ningbo MARSHINE Power Technology Co., Ltd. is a professional engaged in the development, design and manufacture of power engineering construction equipment and tools.
Welcome to contact MARSHINE and reach cooperation, thank you! Earth Anchors,Permanent & Temporary Anchors,Ground Anchors,Heavy Duty Earth Anchors,Screw-In Ground Anchor MARSHINE , https://www.puller-tensioner.com


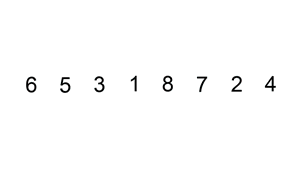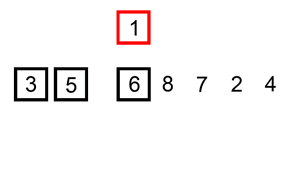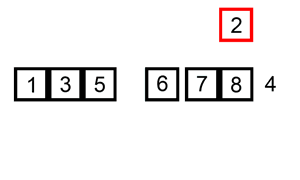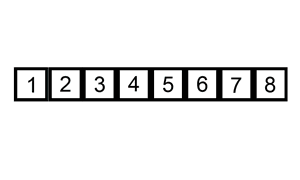

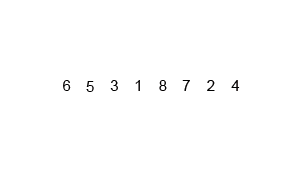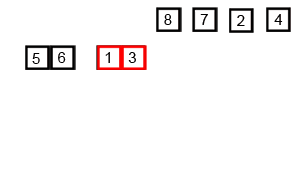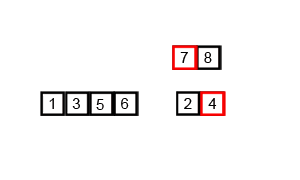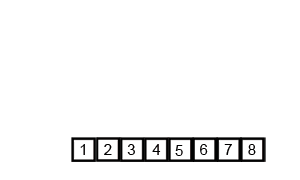

MARSHINE company produces circuit construction tools, including foundation construction, tower group lap. Wiring structure. Cable construction, cable construction, mobile knife mill, insulated overhead cable and high voltage Cable Stripper, all kinds of aluminum alloy pull rod, guide rail, grounding device, high strength shackle, Ratchet Wrench and pointed wrench, double hook tight line device, lifting pulley, nylon wheel and aluminum wheel, punching machine ect.
MARSHINE continues to carry forward the enterprise spirit of "integrity, development, innovation" and strive for the prosperity and development of the electric power industry.