Thermal noise
The thermal noise voltage of the resistor can be expressed as:

R is the resistance, T is the absolute temperature, B is the frequency bandwidth, and k is the Boltzmann constant. At a certain temperature and resistance, thermal noise is generated.
Thermal noise is an intrinsic noise of a resistor that cannot be avoided or eliminated.
The wearer's Thevenin noise model consists of a noise voltage source and a pure resistor, as shown in Figure 1.
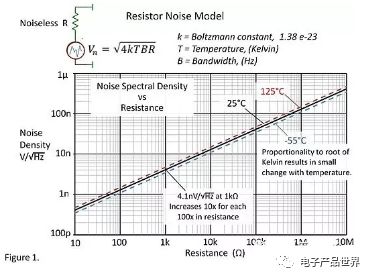
The magnitude of the noise voltage is proportional to the resistance of the resistor, the bandwidth and the square root of the temperature (Kelvin). We usually quantify the noise per 1 Hz bandwidth, which is its spectral density.
Resistance noise is theoretically a "white noise", that is, the noise level is equal within the bandwidth, and the noise is the same in each of the same bandwidths.
The total noise is equal to the sum of the squares of each noise and the square root. The unit of spectral density we often refer to is V/root-Hz. For a 1 Hz bandwidth, this value is equal to the noise level.
For white noise, the spectral density is multiplied by the value after the bandwidth is squared to calculate the total white noise in the bandwidth. In order to measure and quantify the total noise, it is necessary to limit the bandwidth. If you do not know the cutoff frequency, you do not know how wide the band should be integrated.

We all know that the spectrogram is a Bode diagram with the logarithm of the frequency as the x-axis. On the Bode diagram, the bandwidth to the right of the same width is much larger than the left side. From the perspective of total noise, the right side of the Bode diagram may be more important than the left side.
The resistance noise follows a Gaussian distribution, which is a probability density function that describes the amplitude distribution. Obeying the Gaussian distribution is because the resistance noise is generated by a large number of small random events. The central limit theorem explains how it forms a Gaussian distribution. The rms voltage amplitude of the ac noise is equal to the amplitude of the Gaussian distribution distributed over the range of ±1 σ.
For noise with a rms voltage of 1V, the probability of an instantaneous voltage in the range of ±1V is 68% (±1σ). It is often assumed that there is some correlation between white noise and Gaussian distribution, in fact they are not related. For example, the noise of the filter resistor is not white noise but still obeys a Gaussian distribution. Binary noise does not obey the Gaussian distribution, but it is white noise. The resistance noise is both white noise and Gaussian distribution.
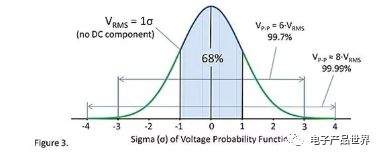
Pure theoretical researchers will think that Gaussian noise does not define peak-to-peak, and it is infinite. This is true, the Gaussian distribution curve is infinitely stretched on both sides, so any voltage peak is possible.
In practice, there are very few rms voltage values ​​that exceed ±3 times the voltage spike. Many people use a 6-fold rms voltage value to approximate the peak-to-peak value. In order to leave enough margin, even 8 times the rms voltage value can be used to approximate the peak-to-peak value.
An interesting problem is that the sum of the noises of the two resistors in series is equal to the noise of the two resistors. Similarly, the sum of the noises of the two resistors in parallel is equal to the noise of the resistors after the two resistors are connected in parallel.
If this is not the case, then there will be problems with series or parallel resistors. Fortunately, it really is like this.
A high value resistor does not generate arcs and sparks due to its own noise voltage. The parasitic capacitance of the resistor is connected across the resistor, limiting its bandwidth and terminal voltage.
Similarly, you can imagine that the high noise voltage generated on the insulator will also be shunted by its parasitic capacitance and surrounding conductors.
Excess noise
The inherent noise of the actual resistance is often much larger than the thermal noise, and the noise exceeding the amplitude of the thermal noise is called excess noise. Unlike thermal noise, excess noise is derived from the discontinuity and non-integrity of the internal structure of the resistor and has a very large relationship with the type of resistor.
The inside of the wirewound resistor is a body metal, and the discontinuity is small, which is the resistance with the smallest excess noise;
The internal structure of the resistance of the composite material is discontinuous, which is the maximum resistance of excess noise;
Inherent noise: wirewound>metal oxide film>metal film>carbon film>glass glaze>synthetic film>synthetic solid.
Ningbo Xingchuangzhi Electric Appliance Co.,Ltd. , https://www.xingchuangzhi.com